Télécommunications
Sources
- Cours, TPs et TDs de Mme.THEYS
- Cours, TPs et TDs de M.PAYAN
- Site Web de M.Mazet
- Animations sur le site de M.Mazet
Bit symbole et valence
Un symbole contient plusieurs bits. Le nombre de bits par symbole est noté n.
Le nombre d'états possibles d'un signal transmis appelé valence est noté M.
On le calcul donc avec la valence (nombre d'états possibles) :
Débit symbole et débit binaire
Le débit symbole est également appelé rapidité de modulation. Le débit symbole est l'inverse du temps symbole :
Débit symbole (en bauds)
Le débit binaire est l'inverse du temps binaire :
Débit binaire (en bits/s)
On peut donc réaliser des conversions entre débit symbole et débit binaire:
Débit binaire en débit symbole en utilisant la Valence (en bits/s)
Éléments de la chaîne de transmission
BER: Bit Error Rate, nombre d'erreur par bitSER: Symbol Error Rate, nombre d'erreur par symbole
1. Le codage source
Le codage source sert à compresser les données à envoyer pour réduire le nombre de bits à transmettre.
2. Le codage canal
Le codage canal sert à ajouter de la redondance dans les données à envoyer. Cela sert à corriger les potentielles erreurs (bruit, interférences…) lors de la transmission.
3. Le modulateur numérique
Le modulateur transmet les bits par paquets, appelés symbole. Les symboles forment un alphabets.
Exemple d'alphabet de 4 symboles : m1 = 00, m2 = 01, m3 = 10, m4 = 11
Le modulateur numérique est constitué de deux éléments :
- le codeur transforme le symbole mk en un jeu de paramètres (ak, Phik)
- le modulateur construit un signal Sk(t) d'une durée Ts (durée symbole) grâce aux paramètres ak et Phik
4. Le canal
Le canal agit comme un filtre passe-bande, de plus, il ajoute du bruit et effectue une distorsion d'amplitude et de phase sur le signal.
Le signal reçu est donc :
Légende :
x(t): signal reçuSpk(t): le signal déformé par le filtre passe-bandew(t): le bruit
5. Le démodulateur numérique
Le démodulateur transforme le signal et une suite de bits.
Le démodulateur numérique est constitué de deux éléments :
- le détecteur retrouve les param^tres (ak, Phik)
- le décodeur reconstruit un symbole à partir du signal x(t) et des paramètres ak et Phik, cette valeur peut être fausse si le signal est dégradé
6. Le décodage canal
Le décodage canal sert à utiliser la redondance mit en place pour corriger les erreurs
7. Le décodage source
Le décodage source décompresse la séquence de bits.
Le signal final pourra être différent du signal source à cause des erreurs
Capacité d'un canal de transmission
Théorème de Shannon-Hartley
Le théorème de Shannon-Hartley permet de connaître la capacité :
Légende :
C: la capacité en bits/sB: la bande occupée en HzS/N: le rapport signal sur bruit(1 + S/N): la valence maximale
Le bruit implique une limitation sur la valence ce qui limit la capacité
On a donc
Légende:
Rb: le débit binaire de la sourceC: la capacité du canal
Théorème de Nyquist
Le théorème de Nyquist définie la largeur de bande minimale pour un canal (pour qu'il n'y est pas d'interférences inter-symboles - IIS)
Légende :
B: la largeur de bandeR: le débit symbole
Comme la bande passante d'un canal est limité, le temp symbole est lui aussi limité donc la rapidité de la transmission est limité
Diagramme de l'oeil
Le diagramme de l'oeil permet de détecter les interférences inter-symboles (IIS).
Pour le tracer, on prend une période (soit T ou 2*T) et on trace le signal sur cette période donnée.
On peut donc mesurer la distance horizontale, aussi appelée "l'ouverture de l'oeil".
Animation du diagramme de l'oeil
Diagramme de constellation
Le diagramme de constellation permet de mesurer l'écart entre les symboles créer par le modem IQ.
Le code de Gray permet de réduire les erreurs, il sert à définir un seul bit différent pour chaque déphase de pi/2
Modulations
Pour transmettre le signal, on le module à l'aide de certains méthodes de modulations.
Si on veut réduire la bande de fréquence occupée par le signal, on utilise des cosinus surélevé ou des gaussiennes au lieu de pulse carré.
On mesure l'efficacité (qu'il faut maximiser) de la modulation à l'aide de la formule suivante :
Légende :
p: l'efficacitéRb: le débit binaire de la sourceB: la largeur de bande
ASK
Amplitude-Shift Keying.
On module en variant l'amplitude
| Fonctionnement |
|---|
 |
FSK
Frequency-Shift Keying (aussi appelé MDF - Modulation par Déplacement de Fréquence).
On module en variant la fréquence
| Fonctionnement |
|---|
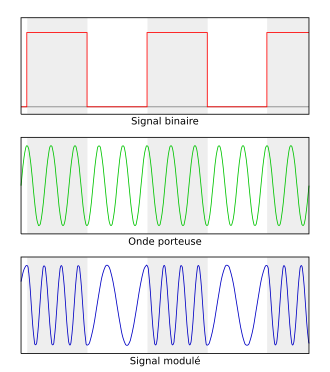 |
MSK
Le MSK (Minimum Shift Keying), utilisé dans lee GSM est une variante du FSK où le signal est démodulé de façon cohérente.
GMSK
Le GMSK (Gaussian Minimum Shift Keying) est une variante du MSK qui utilise un filtre Gaussien pour réduire la largeur de bande.
PSK
Phase-Shift Keying .
On module en variant la phase.
On peut donc choisir plusieurs phases, voici les modulations PSK connus :
BPSK
Binary Phase-Shift Keying. C'est donc une modulation PSK avec seulement deux phases
| Fonctionnement | Diagramme de constellation |
|---|---|
 |
 |
DPSK
Le DPSK est une modulation par phase qui utilise la phase du symbole précédent pour coder un symbole.
QPSK
Quadrature Phase-Shift Keying aussi appelé 4-PSK.
C'est donc une modulation PSK avec quatre phases différentes
| Fonctionnement | Diagramme de constellation |
|---|---|
 |
 |
QAM
Quadrature Amplitude Modulation (en français MAQ - modulation d'amplitude en quadrature).